基础知识-计算机系统

计算机硬件

计算机的基本硬件系统由运算器、控制器、存储器、输入设备和输出设备五大部件组成

运算器、控制器等部件被集成在一起统称为中央处理单元（Central Processing Unit，CPU）。
存储器是计算机系统中的记忆设备，分为内部存储器和外部存储器。
- 内部存储器:速度高、容量小，一般用于临时存放程序、数据及中间结果
- 外部存储器:者容量大、速度慢，可长期保存程序和数据。
输入设备和输出设备合称为外部设备（简称外设），输入设备用于输入原始数据及各种命令，而输出设备则用于输出处理结果

CPU

cpu
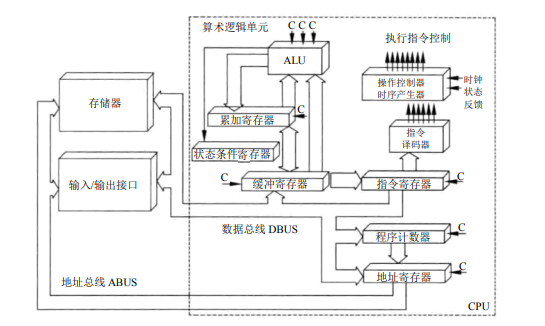
CPU 主要由运算器、控制器、寄存器组和内部总线等部件组成

功能

程序控制：通过执行指令来控制程序的执行顺序
操作控制：一条指令功能的实现需要若干操作信号配合完成，CPU产生每条指令的操作信号并将操作信号送往不同的部件，控制相应的部件按指令的功能要求进行操作
时间控制：CPU对各种操作进行时间上的控制，即在指令执行过程中操作信号的出现时间、持续时间及出现的时间顺序都需要严格的控制
数据处理：CPU通过对数据进行算术运算及逻辑运算等方式进行加工处理，数据加工处理的结果被人们所利用。所以，对数据的加工处理也是CPU最根本的任务。

运算器

运算器由算术逻辑单元、累加寄存器、数据缓存寄存器、状态条件寄存器组成。功能：1.执行所有算术运算2.执行所有的逻辑运算并进行逻辑测试。如与、或、非、零值测试或两个值的比较等

算术逻辑单元（ALU）：负责处理数据，实现对数据的算术运算和逻辑运算
累加寄存器（AC）：也称为累加器，是一个通用寄存器，功能是当运算器的算术逻辑单元执行算术运算或逻辑运算时，为ALU提供一个工作区
数据缓存寄存器（DR）：在对内存储器进行读/写操作时，用DR暂时存放由内存存储器读/写的一条指令或一个数据字，将不同时间段内的读/写数据隔离。主要作用是作为CPU和内存、外部设备之间数据传送中转站；作为CPU和内存、外围设备之间在操作速度上的缓冲；在单累加器结构的运算器中，数据缓冲寄存器还可兼作为操作数据寄存器。
状态条件寄存器（PSW）：由算数指令和逻辑指令运行或测试的结果建立的各种条件码内容，主要分为状态标志和控制标志

控制器

运算器只能完成运算，而控制器用于控制整个 CPU 的工作，它决定了计算机运行过程的自动化。它不仅要保证程序的正确执行，而且要能够处理异常事件。一般包括指令控制逻辑、时序控制逻辑、总线控制逻辑和中断控制逻辑等几个部分。

指令控制逻辑

指令寄存器（IR）: 当 CPU 执行一条指令时，先把它从内存储器取到缓冲寄存器中，再送入 IR 暂存，指令译码器根据 IR 的内容产生各种微操作指令，控制其他的组成部件工作，完成所需的功能。
程序计数器（PC）: 具有寄存信息和计数两种功能，又称为指令计数器。程序的执行分为两种情况，一是顺序执行，二是转移执行。
地址寄存器（AR）: 保存当前 CPU 所访问的内存单元的地址。
指令译码器（ID）: 指令分为操作码和地址码两个部分，为了执行任何给定的命令，必须对操作码进行分析，以便识别所有完成的操作。

时序控制逻辑

为每条指令按时间顺序提供应有的控制信号

总线逻辑

是为多个功能部件服务的信息通路的控制电路。

中断控制

逻辑用于控制各种中断请求，并根据优先级的高低对中断请求进行排队，逐个交给 CPU 处理。

寄存器组

寄存器组分为专用寄存器和通用寄存器。运算器和控制器中的寄存器是专用寄存器，其作用是固定的。通用寄存器的用途广泛，并且由程序员规定其用途，其数目因处理器的不同有所差异。

机器数

各种数值在计算机中表示的形式称为机器数，特点是采用二进制计数制，数的符号用 0 和 1 表示，小数点则隐含，表示不占位置。机器数对应的实际数值称为数的真值。

原码：一个数的正常二进制表示，最高位表示符号。+0(00000000),-0(10000000)
反码：正数的反码即原码，负数的反码是在原码的基础上，除符号位外，其他各位按位取反。+0(00000000),-0(11111111)
补码：正数的补码即原码，负数的补码是在原码的基础上，除符号位外，其他各位按位取反，而后末位+1，若有进位则产生进位。+0 = -0 = 0 0000000
移码：用作浮点运算的阶码，无论正数负数，都是将该原码的补码的首位（符号位）取反得到移码

原码最高位表示正负号，且不参与计数，而其他编码最高位虽然也是代表正负号，但是参与计数

设机器字长为 n，各种码制下带符号数的范围

码制	定点整数	定点小数
原码	$-(2^{n-1}-1)$ ~ $+(2^{n-1}-1)$	$-(1-2^{-(n-1)})$ ~ $+(1-2^{-(n-1)})$
反码	$-(2^{n-1}-1)$ ~ $+(2^{n-1}-1)$	$-(1-2^{-(n-1)})$ ~ $+(1-2^{-(n-1)})$
补码	$-2^{n-1}$ ~ $+(2^{n-1}-1)$	$$-1$$ ~ $+(1-2^{-(n-1)})$
移码	$-2^{n-1}$ ~ $+(2^{n-1}-1)$	$$-1$$ ~ $+(1-2^{-(n-1)})$

浮点数的计算

浮点数：表示方法为 $$N=F*2^E$$ ,其中 E称为阶码，F称为尾数：类似十进制的科学计数法，如 $$85.125=0.85125*10^2$$ ,二进制如： $$101.011=0.101011*2^3$$
在浮点数的表示中，阶码为带符号的纯整数，尾数为带符号的纯小数，要注意符号占最高位（正数0负数1）其表示格式如下所示：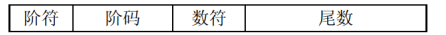

很明显，与科学计数法类似，一个浮点数的表示方法不是唯一的，浮点数所能表示的数值范围由阶码决定，所表示的数值精度由尾数确定。
尾数的表示采用规格化方法，也即带符号尾数的补码必须为1.0xxxx（负数）或者0.1xxxxx（正数），其中x可为0或1
浮点数的运算：对阶（使两个数的阶码相投，小阶向大阶看齐，较小阶码增加几位，尾数就右移动几位）————尾数计算（相加，若是减运算，则加负数）————结果规格化（即尾数表示规格化，带符号尾数转换为1.0xxxx或0.1xxxx）。

算术逻辑和逻辑运算

逻辑与&&：0和1相与，只要有一个0结果为0，两个都为1才为1
逻辑或||：0和1相或，只要有一个为1结果就为1，两个都为0才为0
异或：同0非1，即参加运算的二进制同为0或者同为1结果为0，一个为0另一个为1结果为1
逻辑非！：0的非是1,1的非是0
逻辑左移：二进制整体左移n位，高位若溢出则舍去，低位补0
逻辑右移：二进制整体右移n位，低位若溢出则舍去，高位补0
算术左移算术右移：乘以2或者除以2的算术运算，涉及加减乘除都是算术运算，与逻辑运算区分
短路计算方式： 指通过逻辑运算符（&&、||）左边表达式就能推算出整个表达式的值，不再继续执行逻辑运算右边的表达式
若计算机存储数据采用的是双符号位（00表示正号、11表示负号），两个符号相同的数相加时，如果运算结果的两个符号位经异或运算得1，则可断定这两个数相加的结果产生了溢出。
从计算的角度理解，正数和负数相加其结果肯定不会溢出，如果有溢出，必然同为正数或者同为负数，结果才会更大，有可能溢出，因此，正常两个同符号数相加时，不考虑溢出，其符号位必然还是00或者11，如果有溢出，那么数据位必然最高位进位1，符号位就需要加1，符号位就变为01或者10，因此当符号位为01或者10时数据溢出，观察这两种溢出情况的两个符号位都是一个为0，一个为1，其异或运算运算必然为1，没有其他可能，而逻辑或运算有可能两个都位也能得出1

校验码

在计算机系统运行时，各部位之间要进行数据交换，为了确保数据在传送过程中正确无误，一、是提高硬件电路的可靠性，二是提高代码的校验能力，包括查错和纠错。
码距：就单个编码A：00而言，其码距为1，因为其只需要改变一位就变成另一个编码。在两个编码中，从A码到B码转换所需要改变的位数称为码距，如A：00要转换为B：11，码距为2。一般来说，码距越大，越利于纠错和检错。

奇偶校验码

奇偶校验码:奇偶校验码（Parity Code）是一种简单有效的校验方法。这种方法通过在编码中增加一位校验位，使编码中 1 的个数为奇数（奇校验）或偶数（偶校验），从而使码距变为 2。常用的有水平奇偶校验码、垂直奇偶校验码、水平垂直校验码
奇校验可以可以检测编码中奇数个数位出错，即当合法编码中的奇数位发生了错误时，即编码中的1变成0,或者0变成了1，则该编码中的1的个数的奇偶性就发生了变化，从而检查出错误。但无法纠错。

循环冗余校验码 CRC

循环冗余校验码:循环冗余校验码（Cyclic Redundancy Check，CRC）由两部分组成，左边为信息码（数据），右边为校验码。广泛用于数据通信领域和磁介质存储系统中

CRC只能检错，不能纠错，其原理是找出一个能整除多项式的编码，因此首先要将原始报文除以多项式，将所得的余数作为检验位加在原始报文之后，作为发送数据发给接收方。
使用CRC编码，需要先约定一个生成多项式 $$G(x)$$ 生成多项式的最高位和最低位必须是1。假设原始信息有m位，则对应多项式 $$M(x)$$ .生成检验码思想就是在原始信息位后追加若干检验位，使得追加的信息能被 $$G(x)$$ 整除。接收方接收到带检验位的信息，然后用 $$G(x)$$ 整除余数为0则没有错误，反之则发生错误。

例子：假设原始信息串为10110，CRC的生成多项式为 $$G(x)=x^4+x+1$$ ,求CRC检验码。

(1)在原始信息位后面添0，假设生成多项式的阶为r，则在原始信息位后添加r个0，本题中 $$G(x)$$ 阶为4，则在原始信息串后加4个0，得到新串101100000，作为被除数。
(2)由多项式得到除数，多项中x的幂指数存在的位置1，不存在的位置0，本题中，x的幂指数为0,1,4的变量都存在，而幂指数为2,3的不存在因此得到串10011
(3)生成CRC校验码，将前两步得出的被除数和除数进行模2除法运算（即不进位也不错位的除法运算。过程如下：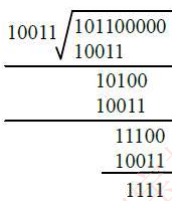

得到余数1111
注意： 余数不足r，则余数左边用若干个0补齐，如求得余数为11，r=4，则补两个0得到0011
(4)生成最终发送信息串，将余数添加到原始信息后。上例中，原始信息为10110，添加余数1111后，结果为101101111。发送方将此数据发送给接收方
(5)接收方进行校验。接收方的CRC检验过程与生成过程类似，接收方接收带检验和的帧后，用多项式 $$G(x)$$ 来除。余数为0则表示信息无措；否则要求发送方重传。
收发信息双发需使用相同的生成多项式

海明校验码

海明码:海明码（Hamming Code）是利用奇偶性来查错和纠错的校验方法。
设数据位是n位，检验位是k位，则n和k必须满足以下关系
$2^{k}-1 \geq {n+k}$
海明码的编码规则如下
设k个检验位为 $P_k,P_{k-1}$ ,……, $$P_1$$ ，n个数据位为 $D_{n-1},D_{n-2}$ ,……, $$D_1,D_0$$ ,对应的海明码为 $H_{n+k},H_{n+k-1}$ ,……, $$H_1$$ ,那么：